|
N-Queens In
2-Dimensions
Here I stake my claim to being the first person to find the guaranteed, algorithmically first-possible solutions (in other words, not the only solutions) for most of the larger boards in this puzzle, up to 49 x 49 squares, and I explain the basis of my claim in detail. I show the exact queen arrangements for each of these first possible solutions, and I invite you to muse with me on their fascinating lack of predictability.
Click the chessboard on the right for my original notes on this 2-dimensional puzzle.
|
 |
|
N-Queens In
3-Dimensions
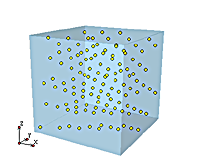
I've been working with my son Martin and his younger sharper intellect to extend this puzzle into the 3rd Dimension (3D). We use the word 'cube' to mean an N-high stack of notional N x N chessboards, and a key feature of these 3D cube solutions is that they are maximally populated. They're maximally populated because under the rules of this puzzle, no additional queens can be placed anywhere inside the cubes. I've written our main solution-search program in C++, and Martin writes PHP programs for his interim searches and analyses, but I've used the free and versatile JavaView Lite utility here to show you three interactive solutions for the following cubes: A. The 11 x 11 x 11
(
or 113
) cube B.
The 133 cube and C. The 313 cube. Click on the cube on the right to see these 3-Dimensional solutions. Our search time for the 313
and larger cubes is significantly reduced thanks to some impressive algorithm
optimisations by Martin.
|
 |
|
Catalytic Conversations On N-Queens
I've written here about some of the programmer's catalytic conversations that Martin and I shared on this project, and on some of our developmental roller-coaster rides as we nudged our algorithm into its current state. |
 |